Ходьба – наиболее естественный вид перемещения человека и наиболее доступный (и безопасный) вид физической нагрузки. Ходьбу можно рассматривать как ряд контролируемых (рефлекторно и автоматизировано) падений. При ходьбе человек опирается последовательно то на одну, то на другую ногу, которая в этот момент является опорной. Другая нога в это время выносится вперед, человек непроизвольно наклоняется и начинает падать, но окончательному падению препятствует выдвинутая вперед нога.
Для амортизации падения подгибается колено выдвинутой вперед ноги, после чего колено распрямляется, и тело (или, вернее, общий центр масс тела ОЦМ, он же общий центр тяжести ОЦТ) возвращается на исходную высоту, после чего все повторяется со сменой ноги.
ОЦТ тела человека находится обычно на уровне II крестцового позвонка, при этом у женщин на 4-5 см ниже, чем у мужчин. (Цитата из фильма «В джазе только девушки»: – Как они ходят на таких каблучищах?! Как они сохраняют равновесие?! – У них центр тяжести в другом месте). У астеников ОЦТ располагается также относительно ниже, чем у гиперстеников.
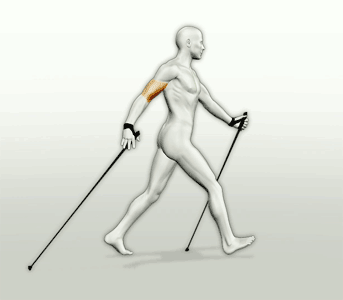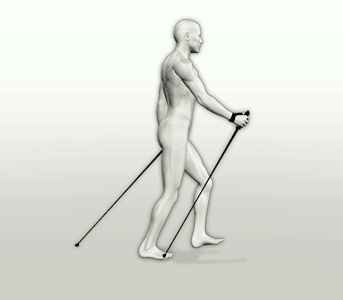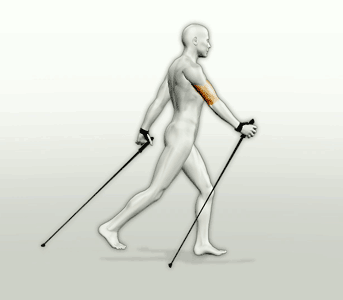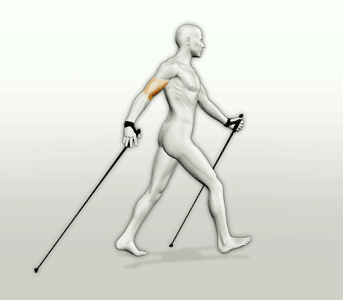
Таким образом, в течение длительности одного шага ОЦТ совершает полный цикл движений «вниз-вверх», центральный рисунок на рисунке ниже. При движении вниз накопленная потенциальная энергия бесполезно расходуется (насчет «бесполезно» уточним позднее), движение вверх требует работы мышц и затрат энергии.
По сути, мы определили общие принципы оценки энерготрат при ходьбе. Исходя из длина ноги и длины шага можно по формулам геометрии (знаменитой теореме Пифагора) рассчитать амплитуду вертикального перемещения ОЦТ, и затем, исходя из веса человека, оценить разницу потенциальных энергий ОЦТ в верхней и нижней точках. А затем попробуем оценить, исходя из КПД мышц, потребную для перемещения на 1 шаг метаболическую энергию.
Отсюда легко определяются энерготраты при преодолении 1 км пути. На рисунке ниже (слева) отображены 2 фазы ходьбы, когда ОЦТ находится в наиболее низком и наиболее высоком положениях.
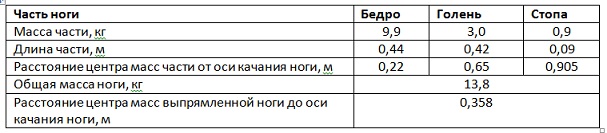
Расчет ведем для некоего «среднего» человека ростом 170 см с длиной шага 74 см и длиной ноги (для наших целей измеряемой от уровня головки бедренной кости до пола, на рисунке от точки шарнирного соединения) 95 см. То, что эта длина чуть больше (на 10 см) половины роста, всегда знали художники (см. правый рисунок пропорций человеческого тела с их точки зрения).
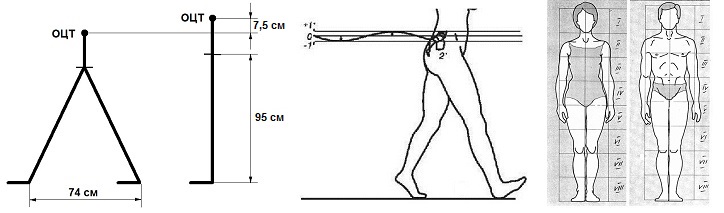
Из рисунка следует, что размах колебаний ОЦТ определяется разницей длины ноги 95 см (т.е. длиной боковых сторон треугольника) и его высотой при раздвинутых на ширину шага ногах. Из теоремы Пифагора следует, что эта разница составляет L = 7,5 см = 0,075 м. При массе человека m = 70 кг его вес (который он вынужден преодолевать при поднятии ОЦТ) составит Вес = g x m = 9,81 х 70 = 687 (Н), (где g =9,81 м\с х с – ускорение свободного падения), а потенциальная энергия ОЦТ изменится на Изм.ПЭ = Вес x L = 687 х 0,075 = 52 (Дж).
Чтобы пройти 1 км, человеку необходимо сделать 1000/0,74 = 1350 шагов, и сумма изменений потенциальной энергии составит 1350 х 52 = 70.000 (Дж), или 70 кДж. Далее мы вступаем в зону неопределенности, поскольку не знаем точно, каков КПД человека при ходьбе. КПД мышц нетренированного человека не превышает 25%, но следует считаться с тем, что при ходьбе совершаются постоянные компенсирующие движения, минимизирующие вертикальные перемещения, и обеспечивающие плавность ходьбы. В итоге расход энергии также минимизируется и составляет уже не 70/0,25 = 280 (кДж/км), как получается по нашей схеме, а меньше.
В реальности, вследствие компенсирующих движений (о них другим постом), размах колебаний ОЦТ составляет всего 5 см, и пересчитанный расход равен 185 кДж/км. Переведем килоджоули в более привычные нам килокалории, исходя из соотношения 1 кДж = 0,239 ккал. 0,239 х 185 = 44 (ккал/км). ОЦМ смещается также в сторону на 2,5 см, на затраты энергии на это не сравнимы с затратами на подъем ОЦТ.
Существует еще одно обстоятельство, уменьшающее энерготраты при ходьбе – рекуперация энергии за счет упругой деформации мышц нижней конечности. При рекуперации часть энергии сохраняется путем перехода кинетической энергии в потенциальную энергию гравитации и обратно.
Наиболее точно энерготраты на ходьбу можно определить путем инструментальных измерений, методами непрямой калориметрии, с учетом поглощенного из вдыхаемого воздуха кислорода и количества выделяемого углекислого газа. Специальные аппараты (респирометры) позволяют по анализу газообмена оценить затраты на многие виды работ в условиях, приближенных к реальным.
Результатами подобных измерений пользуются производители тренажеров «беговая дорожка», которые заинтересованы в том, чтобы показания дисплея тренажера соответствовали реальным энерготратам. Проведенные нами сравнения тренажеров разных марок показали, что между ними сохраняется высокое соответствие в показаниях, т.е. во все тренажеры зашит схожий алгоритм оценки энерготрат.
Вот достаточно типичные данные: при задании веса человека 70 кг на скорости 3 км/ч энерготраты составляют 175 ккал/ч, а при скорости 6 км/ч - уже 286 ккал/ч. При первом рассмотрении создается впечатление, что сделанный нами вывод о независимости энерготрат на 1 км пути от скорости неверен, поскольку в первом случае затраты на 1 км составляют 175/3 = 58 (ккал/км), а во втором 286/6 = 48 (ккал/км)
.
Вопрос же заключается в том, с какой стороны нас интересуют энерготраты при ходьбе. Если для расчета суточных энерготрат человека методом факторного анализа всех видов энерготрат за сутки, то нас должны интересовать часовые затраты на разные виду деятельности с включением в них энергии основного обмена, если же эффективность нашей физической активности с целью тренировки аэробных возможностей и/или жиросжигания, то без основного обмена.
Затраты на основной обмен человека весом 70 кг исходя из энероготрат покоя ЭТП мужчин 1 ккал/час/кг и женщин 0,9 ккал/час/кг (берем среднее значение 0,95 ккал/час/кг) составят порядка 66 ккал/ч, и затраты на собственно ходьбу составят в первом случае 175 – 66 = 109 (ккал), а во втором 286 – 66 = 220 (ккал), откуда затраты на 1 км пути при скорости 3 км/ч составят 109/3 = 36 (ккал), а при скорости 6 км/ч – 220/6 = 37 (ккал).
Вы еще не забыли, что вес человека принят за 70 кг? Энерготраты на 1 км составили (численно) половину от веса. Отсюда простое правило:
Энерготраты на ходьбу в ккал равны произведению половины веса в кг на пройденное в км расстояние.ЭТ = 0,5 х Вес х Расстояние
Выше, исходя из геометрических расчетов и простой схемы движения ног (схожей с качаниями маятника), мы нашли значение коэффициента в формуле 0,239 х 280/70 = 0,96 (ккал/кг/км), поправка на компенсирующие движения, уменьшающие размах колебаний ОЦТ до 5 см, дает значение 44/70 = 0,63 (ккал/кг/км), по результатам инструментальных измерений значение принимаем равным 0,50 ккал/кг/км, (сказывается рекуперация энергии и учтен некий усредненный КПД мышц, условно принятый нами за 25%).
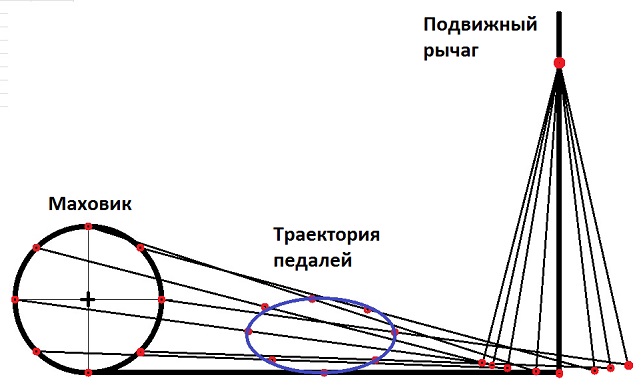
В конце концов, человек изобрел самокат и велосипед также для того, чтобы избавиться от бесполезного с точки зрения энергосбережения колебания ОЦТ.
Все оценочные расчеты мы привели на численном примере для некоего среднего человека среднего роста, со средними длиной ноги, длиной шага и весом. Но вес уже учтен в формуле, которая справедлива для произвольного веса, и формула справедлива также при изменении длины ноги (пропорционально изменится длина шага, обратно пропорционально изменится количество шагов на 1 км пути, и конечное соотношение не изменится.
Итак, для целей фитнеса и жиросжигания нет смысла пользоваться таблицами энеготрат на ходьбу в зависимости от скорости ходьбы, где приводятся данные в расчете на 1 минуту или 1 час. Эти таблицы противоречивы, зачастую скомпилированы из разных источников, и значения приведены лишь для нескольких значений скорости, да и зачем эту скорость знать, если вы совершаете пешую прогулку для настроения (и с тайной мыслью сжечь побольше калорий, чтобы заработать побольше вкусной еды).
Для оценки энерготрат (без основного обмена) достаточно знать километраж прогулки, для чего в помощь масштабные карты-схемы городов и всевозможные фитнес-трекеры, позволяющие отсчитывать пройденное расстояние. При этом простые модели по факту отсчитывают пройденные шаги, а модели с GPS непосредственно пройденное расстояние.
Простые модели без GPS зачастую ошибаются в подсчете числа шагов (могут пропустить шаг или посчитать один шаг за 2, их показания зависят от походки и покрытия дороги), они не знают длину вашего шага (оценивают по введенному росту), а при подсчете калорий вдобавок плюсуют к энерготратам на ходьбу энерготраты на основной обмен.
Другой вопрос – с какой скоростью следует ходить. Ответ один – с комфортной для себя. Вопросов тренировочного воздействия ходьбы мы здесь касаться не будем, для здоровья полезна любая ходьба, здравый смысл и интуиция подскажут необходимую скорость. Дополнительный контроль по частоте пульса – про то в другой раз.
Разумеется, приведенная оценка приближенная, и в первую очередь оттого, что при изменении скорости ходьбы меняется и длина шага (увеличивается с увеличением скорости). Но здесь примечательно то, что зависимость не прямо пропорциональная, а сглаженная, прямо пропорциональная корню квадратному из скорости, т.е. при увеличении скорости в 2 раза длина шага увеличивается в 1,4 раза, что приводит к увеличению размаха ОЦТ также в 2 раза. Но при этом в 1,4 раза уменьшается число шагов на 1 км пути, и энерготраты на километр пути возрастут всего лишь в 1,4 раза, т.е. далеко не пропорционально скорости.
Вдобавок усилится эффект компенсирующих движений, и с учетом того, что непрофессионал (не спортсмен) перемещается со скоростью от 3 км/ч (что считается замедленным темпом) до 6 км/ч (ускоренный темп), с зависимостью энерготрат от скорости не следует считаться – не учтенные нами факторы вносят заведомо большую погрешность. Для нас достаточно и того, что систематическая погрешность вследствие индивидуальных особенностей энергетики мышц, походки всегда одна и та-же, а нас интересует динамика и прогресс.
Немного о встречающихся в литературе и на сайтах иных рекомендациях. О таблицах мы уже говорили, но есть рекомендация оценивать энерготраты при ходьбе из расчета 0,8 ккал/кг/км. Обоснование этого значения нам неизвестно, но оно также основано на зависимости энерготрат лишь от веса и километража. Впрочем, оно становится справедливым (и совпадает с рекомендованным нами) при условии, что в энерготраты включен основной обмен, а скорость ходьбы составляет 2,7 км/ч, примерно на нижней границе рассматриваемого нами интервала скоростей ходьбы. В общем случае для наших целей эта формула заведомо не годится.
Встречается также рекомендация выполнять расчет энерготрат на ходьбу по формуле
E = 0,007 x V x V +21 (кал/мин/кг)
где V – скорость в м/мин, а E – энерготраты в кал/мин/кг. После перехода к скорости в км/ч, от минут к часам, а от калорий к килокалориям формула преобразуется:
E = 0,117 x V x V + 1,26 (ккал/час/кг)
Поскольку в эту формулу также включен основной обмен, вычтем из нее среднюю величину энерготрат покоя 0,95 ккал/час/кг, получаем
ЭТ = 0,117 x V x V + 0,31
В расчете на 1 км пути получаем
ЭТкм = 0,117 x V + 1,26/V (ккал/кг)
Формула интересна тем, что первый член с ростом скорости растет, а второй уменьшается, что некоторым образом взаимно компенсируется.
В интересующем нас диапазоне скоростей ходьбы от 3 до 6 км/ч значение изменяется от 0,454 до 0,754 ккал/кг/км. Достаточно близкое соответствие принятому нами постоянному коэффициенту 0,5 ккал/кг/км, и полное совпадение при скорости порядка 3,5 км/ч, считающейся средней для неспешной ходьбы.
Не исключено, что последняя формула с квадратичной зависимостью более точна, и рассчитана на более широкий диапазон скоростей, чем принятый нами, с распространением на профессиональных спортсменов-ходоков, и учетом длины шага от скорости. Для любителей же вполне пригодно приведенное нами упрощенное соотношение.