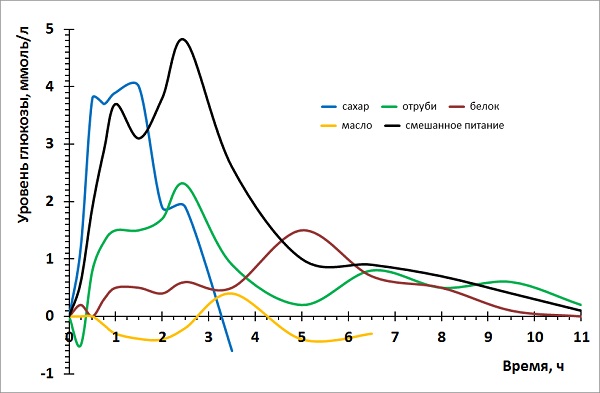
Тогда УОО будет пропорционален росту во 2-й степени или весу в степени 2/3. Но люди не являются масштабными копиями некоторой модели, в противном случае не существовало бы деление людей по типам фигур: яблоко (круг, овал, ромб), груша (треугольник), банан (прямоугольник, линейка), клубника (перевернутый треугольник), песочные часы. И даже при одинаковости типа фигуры люди могут различаться по составу тела (проценту жировой массы) и возрасту (с возрастом уровень обменных процессов уменьшается).
Формула расчета (прогноза) УОО должна учесть рост, вес, возраст и пол, притом для простоты расчета и понимания формулы желательно, чтобы все перечисленные переменные входили в формулу порознь и в первой степени – нежелательны члены с перемножением переменных и возведением их в степень (целочисленную или дробную). Формула должна представлять собой сумму переменных с отличными для каждой переменной коэффициентами, в общем случае и отрицательными.
Первая подобная формула УОО – формула Харриса и Бенедикта с разными коэффициентами для мужчин и женщин при росте, возрасте и весе, и отличными свободными членами. Вот эти формулы:
Для мужчин УОО = 13,75 М + 5,00 Р - 6,76 В + 66
Для женщин УОО = 9,56 М + 1,85 Р - 4,68 В + 655
где УОО – уровень основного обмена в ккал, М – масса (вес) тела в кг, Р – рост в см, В – возраст в годах.
То, что свободный член 66 для мужчин и 655 для женщин – источник непонимания, а иногда даже ошибок при копировании и размещении формул – отчего УОО мужчин якобы меньше УОО женщин, когда все знают, что соотношение обратное.
Тут мы касаемся технологии создания формул т.н. множественной регрессии. Есть полученный в исследовании набор данных – для множества людей измерены УОО и 4 переменные – рост, вес, возраст и пол. А затем путем применения некоторого математического формализма определяются коэффициенты при переменных, при которых теоретический (вычисленный по формуле) УОО минимально отклоняется от экспериментального по всему множеству участников эксперимента.
Это решение очень неустойчиво вследствие того, что т.н. «независимые» переменные независимыми не являются – вес зависит от роста (вспомним знаменитую формулу Брока Вес = Рост минус 100), рост хоть и в малой степени, но зависит от пола (женщины в среднем на 14 см ниже мужчин). Неустойчивость решения заключается в том, что при малом изменении в составе группы обследованных, возможны значительные изменения в коэффициентах при переменных. Притом никоим образом не одного коэффициента – изменяются разом все коэффициенты и свободный член, перетекая один в другой или «вбирая» друг друга.
В итоге значения коэффициентов достаточно случайны, и смысл имеет лишь данный набор коэффициентов. Даже при первом взгляде на 2 формулы Х.-Б. (для мужчин и женщин) удивление вызывает огромный разрыв в значениях свободного члена (для женщин на 589 ккал больше, чем для мужчин), при том, что УОО женщин ниже УОО мужчин в среднем на 200 ккал.
Что же компенсирует эту огромную невязку в 800 ккал? Да на 4,1 ккал/кг меньший коэффициент при весе и на 3,2 ккал/см меньший коэффициент при росте. Коэффициенты при возрасте достаточно близки (у женщин меньше, чем у мужчин), на то есть причины – возраст независим от роста и веса, а УОО женщин меньше УОО мужчин, да и интенсивность снижения процессов метаболизма у них разная.
А теперь умножим разницу коэффициентов 4,1 на средний вес 70, а разность 3,2 на средний рост 170, и сложим 2 произведения – получаем 831 ккал. Все сходится, невязка в 800 ккал находит объяснение. Понимание вышесказанного позволяет понять и даже спрогнозировать, что повтор исследования Х.-Б. приведет к получению формулы с совершенно иными коэффициентами, но схожими результатами расчета по формуле.
Подобное и было сделано в 1990 г Миффлином и СанЖеором. Исследователи, идя традиционным путем, выработали 2 формулы (для мужчин и женщин):
Для мужчин УОО = 9,98 М + 7,94 Р - 5,41 В - 273
Для женщин УОО = 9,91М + 4,26 Р - 4,38 В + 149
Понимая всю условность и случайность значений коэффициентов и свободных членов, исследователи предложили уравнять коэффициенты в 2 формулах, и тогда всю разницу в УОО вбирает в себя свободный член:
Для мужчин УОО = 9,99 М + 6,25 Р - 4,92 В + 5
Для женщин УОО = 9,99 М + 6,25 Р - 4,92 В - 161
Здесь все становится на свои места: разница в свободных членах непосредственно является разницей в УОО между мужчинами и женщинами.
Затем авторы идут еще дальше: для удобства вычислений округляют коэффициенты в формулах, проявив некоторое недопонимание и не изменив соответственно свободные члены.
Для мужчин УОО = 10 М + 6,25 Р - 5 В + 5
Для женщин УОО = 10 М + 6,25 Р - 5 В - 161
То, что коэффициент 6,25 оставлен неизменным, отражает менталитет человека западного мира, где счет идет на дюжины, и округлением считается округление до ближайшей четвертушки. С нашей точки зрения, вполне можно было бы округлить коэффициент 6,25 до целочисленного 6, изменив примерно на 40-45 ккал значения свободных членов в сторону увеличения (не произвольно, а по результатам матобработки первичных данных).
А теперь выведем для целей МФ удобную на практике формулу, с учетом всего вышесказанного, располагая свободой в округлении и даже выборе коэффициентов при переменных. В 5 формулах (2 формулы Х.-Б. и 2 формулы М.-СЖ. отдельно для мужчин и женщин и общая для мужчин и женщин формула М.-СЖ. Коэффициент при весе меняется в пределах от 9,56 до 13,75, при росте от 1,85 до 7,94, при возрасте от -4,38 до -6,8.
Обращаем внимание на схожесть коэффициентов при росте и весе, при этом интервал коэффициентов при возрасте (по модулю) лежит полностью в пределах интервала коэффициентов при росте. Возможно произвольное назначение любого коэффициента в этих пределах, выбираем целочисленные значения 6 для роста и -6 для возраста. Мгновенно конструируется часть формулы УОО в виде 6(Р-В). Для коэффициента при весе просматриваются варианты 10; 11; 12; 13. Возможен выбор любого из этих значений (хотя из самых общих сображений предпочтительны центральные значения 11 или 12), под выбранное значение подтянется значение свободного члена.
За основу подгонки нашей формулы берем формулу М.-СЖ. как более современную, учитывающую особенности обмена, питания и физактивности наших современников. 2 контрольные точки задаются средним весом мужчин по исследованию 87,5 кг и женщин 70,2 кг, средним ростом мужчин 178,3 см и женщин 164,2 см, и средним возрастом мужчин 44,4 года и женщин 44,6 лет.
Подсчитаем по формулам М.-СЖ. УОО «средних» по исследованию
мужчины УОО = 9,98 х 87,5 + 7,94 х 178,3 – 5,41 х 44,4 -273 = 1776 (ккал)
и женщины УОО = 9,91 х 70,2 + 4,26 х 164,2 – 4,38 х 44,6 + 149 = 1349 (ккал).
По части формулы 6(Р-В) и вариантам коэффициента при весе 10; 11; 12 и 13 определяем для «средних» людей свободные члены.

Беглый взгляд на таблицу выявляет, что наиболее оптимальным выбором явится значение коэффициента при весе 11 со свободными членами 10 для мужчин и -141 для женщин. Но 10 ккал настолько малая величина в сравнении с погрешностями формул УОО, что ею пренебрегаем, а значение -141 тоже изменяем на 10 ккал и округляем. Итоговые формулы УОО для практики МФ:
Для мужчин УОО = 6 х (Р-В) + 11 х М
Для женщин УОО = 6 х (Р-В) + 11 х М – 150.
Эти формулы (легко запоминаемые и пригодные для устного счета) были предложены нами несколько лет назад и с успехом использовались для подсчета энерготрат на МФ, с добавлением к ним отдельно подсчитываемых калорий физической активности. Впрочем, исходя из практики МФ, эти формулы следует подправить. Не оттого, что они неверны – оттого, что их стали применять в области, где их применение нецелесообразно.
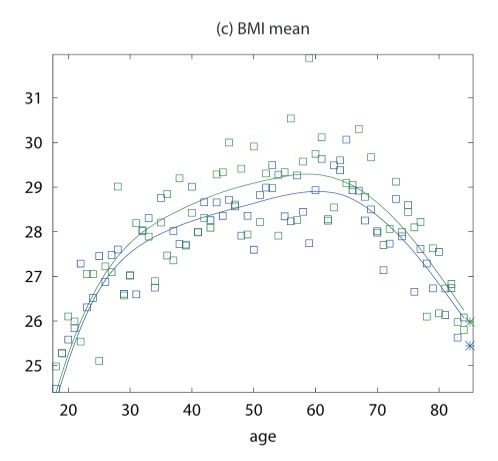
Средний индекс массы тела ИМТ по исследованию М.-СЖ.
мужчин ИМТ = 87,5/(1,783 х 1,783) = 27,5
женщин ИМТ = 70,2/(1,642 х 1,642) = 26,03
т.е. формула М.-СЖ. (и соответственно формула МФ) наиболее точна на людях с избыточным весом (ИМТ от 25 до 30). Для людей с нормальным и недостаточным весом расчет даст заниженное значение, для людей с ожирением тем более завышенное, чем выше степень ожирения.
Следующим постом мы предложим более универсальную формулу, пригодную в широком диапазоне веса, включая недостаточный и нормальный вес и ожирение.